Matrices

A matrix represents a collection of numbers arranged in an order of rows and columns. It is necessary to enclose the elements of a matrix in parentheses or brackets.

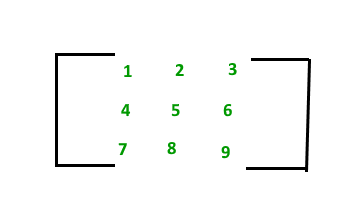
A matrix with 9 elements is shown below.

This Matrix [M] has 3 rows and 3 columns. Each element of matrix [M] can be referred to by its row and column number. For example, a23=6

Order of a Matrix :

The order of a matrix is defined in terms of its number of rows and columns.

Order of a matrix = No. of rows ×No. of columns

Therefore Matrix [M] is a matrix of order 3 × 3.

Transpose of a Matrix :

The transpose [M]T of an m x n matrix [M] is the n x m matrix obtained by interchanging the rows and columns of [M].

if A= [aij] mxn , then AT = [bij] nxm where bij = aji

Properties of transpose of a matrix:

• (A^T)^T = A
• (A+B)^T = A^T + B^T
• (AB)^T = B^TA^T

Singular and Nonsingular Matrix:

1. Singular Matrix: A square matrix is said to be singular matrix if its determinant is zero i.e. |A|=0
2. Nonsingular Matrix: A square matrix is said to be non-singular matrix if its determinant is non-zero.

Square Matrix: A square Matrix has as many rows as it has columns. i.e. no of rows = no of columns.